Common options
All models follow the same approach: the standard curve is fitted on its own first and the results are derived from a model parallel to that of the reference but fitted on the quality control or test sample.
Analysis options
Transformation of the dose
The estimation of the result assumes the dose will be analysed on a log scale. If the data for dose levels are not already presented on the log scale, the following log scale transformations are available:
• log base 2
• log base e
• log base 10
Transformation of the response
A log transformation of the response can often result in more stable variance across the range of dose levels in the assay. The response can be transformed as follows:
• log base 2
• log base e
• log base 10
• square root
• square
It is also possible to apply a linear transformation to the response. This allows an offset to be added to the recorded dose, and a constant multiplier to be applied.
Outlier identification and removal
QuBAS allows for examination of the data for outliers, and the option to exclude the outliers. There are two options for the identification
• Grubb’s test: significance level fixed at p = 0.05
• Studentised residuals: outlier if it is larger than 3
Method for ratios
There are 2 generally used methods for calculating confidence limits for ratio values.
• Delta Method: based on a truncated Taylor series expansion (generally applicable to any function of random variables).
• Fieller Method: developed specifically for ratios of random variables.
Variance estimate
The confidence intervals for QC and test samples, and for the result, are calculated with the pooled variance.
That is, the variance for the one-parameter fit is
The 1x1 Hessian is scaled using this variance.
This provides a consistent approach between having a unique data point (in which case the variance would not be defined) and having multiple data points. It assumes the same variance in the responses for the reference and the sample considered, which is reasonable assuming they are on the same plate.
System Suitability Criteria
Controls
Upper and lower limits can be set for the mean or geometric mean of:
• All control samples
• By groups if present e.g. high, low
Specific management of spiked samples is not implemented in this version, but is planned for future release.
Reference standard
Variability of data
An upper limit for the variance,
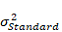
, can be set.
An upper limit for the root mean square error (RMSE) can be set.
Quality Controls
Range and Equivalence tests for the result
• The user specifies the range for the estimated concentration or the range for its confidence interval.
Parallelism: significance test
The fit is parallel by construction so an approximate F test is used instead.
• F statistic = (test sum of squares) / (reference sum of squares)
• Degrees of freedom for the test sample = number of dilutions - 1.
• Degrees of freedom for the reference = number of concentrations - number of parameters (1 for the linear model, 4 for 4PL and 5 for 5PL).
This assumes the test data is only used to fit the intercept of the QC sample, and the reference data is only used to fit the other parameters. This is approximately true.
Variability of data
An upper limit for the variance,
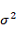
, can be set. An upper limit for the root mean square error (RMSE) can be set.
Precision
An upper limit for the precision (the ratio of the upper limit and the lower limit of the confidence interval of the result). This requires:
• the upper limit
• the confidence level for the interval
Sample Suitability Criteria
With this method there are only two criteria that need to be tested for the sample
1. Do the data points lie on a curve that is parallel to the standard? This is tested by a goodness of fit test
2. Is the estimate sufficiently precise to be used? This is tested by the precision (ratio of the ratio of the upper limit and the lower limit of the confidence interval of the result).
Parallelism: significance test
The fit is parallel by construction so an approximate F test is used instead.
• F statistic = (test sum of squares) / (reference sum of squares)
This assumes the test data is only used to fit the intercept of the test sample, and the reference data is only used to fit the other parameters.
Variability of data
An upper limit for the variance,
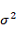
, can be set. An upper limit for the root mean square error (RMSE) can be set.
Precision
An upper limit for the precision (the ratio of the upper limit and the lower limit of the confidence interval of the result).